Quantitative Economics with Python
Linear Regression in Python
57. Linear Regression in Python¶
Contents
In addition to what’s in Anaconda, this lecture will need the following libraries:
!pip install linearmodels
Collecting linearmodels
Downloading linearmodels-4.22-cp38-cp38-manylinux1_x86_64.whl (1.5 MB)
?25l
|▎ | 10 kB 33.5 MB/s eta 0:00:01
|▌ | 20 kB 36.5 MB/s eta 0:00:01
|▊ | 30 kB 24.6 MB/s eta 0:00:01
|█ | 40 kB 10.0 MB/s eta 0:00:01
|█▏ | 51 kB 11.9 MB/s eta 0:00:01
|█▍ | 61 kB 13.6 MB/s eta 0:00:01
|█▋ | 71 kB 11.7 MB/s eta 0:00:01
|█▉ | 81 kB 13.0 MB/s eta 0:00:01
|██ | 92 kB 12.6 MB/s eta 0:00:01
|██▎ | 102 kB 11.0 MB/s eta 0:00:01
|██▌ | 112 kB 11.0 MB/s eta 0:00:01
|██▊ | 122 kB 11.0 MB/s eta 0:00:01
|███ | 133 kB 11.0 MB/s eta 0:00:01
|███▏ | 143 kB 11.0 MB/s eta 0:00:01
|███▍ | 153 kB 11.0 MB/s eta 0:00:01
|███▋ | 163 kB 11.0 MB/s eta 0:00:01
|███▉ | 174 kB 11.0 MB/s eta 0:00:01
|████ | 184 kB 11.0 MB/s eta 0:00:01
|████▎ | 194 kB 11.0 MB/s eta 0:00:01
|████▌ | 204 kB 11.0 MB/s eta 0:00:01
|████▊ | 215 kB 11.0 MB/s eta 0:00:01
|█████ | 225 kB 11.0 MB/s eta 0:00:01
|█████▏ | 235 kB 11.0 MB/s eta 0:00:01
|█████▍ | 245 kB 11.0 MB/s eta 0:00:01
|█████▋ | 256 kB 11.0 MB/s eta 0:00:01
|█████▉ | 266 kB 11.0 MB/s eta 0:00:01
|██████ | 276 kB 11.0 MB/s eta 0:00:01
|██████▎ | 286 kB 11.0 MB/s eta 0:00:01
|██████▌ | 296 kB 11.0 MB/s eta 0:00:01
|██████▊ | 307 kB 11.0 MB/s eta 0:00:01
|███████ | 317 kB 11.0 MB/s eta 0:00:01
|███████▏ | 327 kB 11.0 MB/s eta 0:00:01
|███████▍ | 337 kB 11.0 MB/s eta 0:00:01
|███████▋ | 348 kB 11.0 MB/s eta 0:00:01
|███████▉ | 358 kB 11.0 MB/s eta 0:00:01
|████████ | 368 kB 11.0 MB/s eta 0:00:01
|████████▎ | 378 kB 11.0 MB/s eta 0:00:01
|████████▌ | 389 kB 11.0 MB/s eta 0:00:01
|████████▊ | 399 kB 11.0 MB/s eta 0:00:01
|█████████ | 409 kB 11.0 MB/s eta 0:00:01
|█████████▏ | 419 kB 11.0 MB/s eta 0:00:01
|█████████▍ | 430 kB 11.0 MB/s eta 0:00:01
|█████████▋ | 440 kB 11.0 MB/s eta 0:00:01
|█████████▉ | 450 kB 11.0 MB/s eta 0:00:01
|██████████ | 460 kB 11.0 MB/s eta 0:00:01
|██████████▎ | 471 kB 11.0 MB/s eta 0:00:01
|██████████▌ | 481 kB 11.0 MB/s eta 0:00:01
|██████████▊ | 491 kB 11.0 MB/s eta 0:00:01
|███████████ | 501 kB 11.0 MB/s eta 0:00:01
|███████████▏ | 512 kB 11.0 MB/s eta 0:00:01
|███████████▍ | 522 kB 11.0 MB/s eta 0:00:01
|███████████▋ | 532 kB 11.0 MB/s eta 0:00:01
|███████████▉ | 542 kB 11.0 MB/s eta 0:00:01
|████████████ | 552 kB 11.0 MB/s eta 0:00:01
|████████████▎ | 563 kB 11.0 MB/s eta 0:00:01
|████████████▌ | 573 kB 11.0 MB/s eta 0:00:01
|████████████▊ | 583 kB 11.0 MB/s eta 0:00:01
|█████████████ | 593 kB 11.0 MB/s eta 0:00:01
|█████████████▏ | 604 kB 11.0 MB/s eta 0:00:01
|█████████████▍ | 614 kB 11.0 MB/s eta 0:00:01
|█████████████▋ | 624 kB 11.0 MB/s eta 0:00:01
|█████████████▉ | 634 kB 11.0 MB/s eta 0:00:01
|██████████████ | 645 kB 11.0 MB/s eta 0:00:01
|██████████████▎ | 655 kB 11.0 MB/s eta 0:00:01
|██████████████▌ | 665 kB 11.0 MB/s eta 0:00:01
|██████████████▊ | 675 kB 11.0 MB/s eta 0:00:01
|███████████████ | 686 kB 11.0 MB/s eta 0:00:01
|███████████████▏ | 696 kB 11.0 MB/s eta 0:00:01
|███████████████▍ | 706 kB 11.0 MB/s eta 0:00:01
|███████████████▋ | 716 kB 11.0 MB/s eta 0:00:01
|███████████████▉ | 727 kB 11.0 MB/s eta 0:00:01
|████████████████ | 737 kB 11.0 MB/s eta 0:00:01
|████████████████▎ | 747 kB 11.0 MB/s eta 0:00:01
|████████████████▌ | 757 kB 11.0 MB/s eta 0:00:01
|████████████████▊ | 768 kB 11.0 MB/s eta 0:00:01
|█████████████████ | 778 kB 11.0 MB/s eta 0:00:01
|█████████████████▏ | 788 kB 11.0 MB/s eta 0:00:01
|█████████████████▍ | 798 kB 11.0 MB/s eta 0:00:01
|█████████████████▋ | 808 kB 11.0 MB/s eta 0:00:01
|█████████████████▉ | 819 kB 11.0 MB/s eta 0:00:01
|██████████████████ | 829 kB 11.0 MB/s eta 0:00:01
|██████████████████▎ | 839 kB 11.0 MB/s eta 0:00:01
|██████████████████▌ | 849 kB 11.0 MB/s eta 0:00:01
|██████████████████▊ | 860 kB 11.0 MB/s eta 0:00:01
|███████████████████ | 870 kB 11.0 MB/s eta 0:00:01
|███████████████████▏ | 880 kB 11.0 MB/s eta 0:00:01
|███████████████████▍ | 890 kB 11.0 MB/s eta 0:00:01
|███████████████████▋ | 901 kB 11.0 MB/s eta 0:00:01
|███████████████████▉ | 911 kB 11.0 MB/s eta 0:00:01
|████████████████████ | 921 kB 11.0 MB/s eta 0:00:01
|████████████████████▎ | 931 kB 11.0 MB/s eta 0:00:01
|████████████████████▌ | 942 kB 11.0 MB/s eta 0:00:01
|████████████████████▊ | 952 kB 11.0 MB/s eta 0:00:01
|█████████████████████ | 962 kB 11.0 MB/s eta 0:00:01
|█████████████████████▎ | 972 kB 11.0 MB/s eta 0:00:01
|█████████████████████▌ | 983 kB 11.0 MB/s eta 0:00:01
|█████████████████████▊ | 993 kB 11.0 MB/s eta 0:00:01
|██████████████████████ | 1.0 MB 11.0 MB/s eta 0:00:01
|██████████████████████▏ | 1.0 MB 11.0 MB/s eta 0:00:01
|██████████████████████▍ | 1.0 MB 11.0 MB/s eta 0:00:01
|██████████████████████▋ | 1.0 MB 11.0 MB/s eta 0:00:01
|██████████████████████▉ | 1.0 MB 11.0 MB/s eta 0:00:01
|███████████████████████ | 1.1 MB 11.0 MB/s eta 0:00:01
|███████████████████████▎ | 1.1 MB 11.0 MB/s eta 0:00:01
|███████████████████████▌ | 1.1 MB 11.0 MB/s eta 0:00:01
|███████████████████████▊ | 1.1 MB 11.0 MB/s eta 0:00:01
|████████████████████████ | 1.1 MB 11.0 MB/s eta 0:00:01
|████████████████████████▏ | 1.1 MB 11.0 MB/s eta 0:00:01
|████████████████████████▍ | 1.1 MB 11.0 MB/s eta 0:00:01
|████████████████████████▋ | 1.1 MB 11.0 MB/s eta 0:00:01
|████████████████████████▉ | 1.1 MB 11.0 MB/s eta 0:00:01
|█████████████████████████ | 1.1 MB 11.0 MB/s eta 0:00:01
|█████████████████████████▎ | 1.2 MB 11.0 MB/s eta 0:00:01
|█████████████████████████▌ | 1.2 MB 11.0 MB/s eta 0:00:01
|█████████████████████████▊ | 1.2 MB 11.0 MB/s eta 0:00:01
|██████████████████████████ | 1.2 MB 11.0 MB/s eta 0:00:01
|██████████████████████████▏ | 1.2 MB 11.0 MB/s eta 0:00:01
|██████████████████████████▍ | 1.2 MB 11.0 MB/s eta 0:00:01
|██████████████████████████▋ | 1.2 MB 11.0 MB/s eta 0:00:01
|██████████████████████████▉ | 1.2 MB 11.0 MB/s eta 0:00:01
|███████████████████████████ | 1.2 MB 11.0 MB/s eta 0:00:01
|███████████████████████████▎ | 1.2 MB 11.0 MB/s eta 0:00:01
|███████████████████████████▌ | 1.3 MB 11.0 MB/s eta 0:00:01
|███████████████████████████▊ | 1.3 MB 11.0 MB/s eta 0:00:01
|████████████████████████████ | 1.3 MB 11.0 MB/s eta 0:00:01
|████████████████████████████▏ | 1.3 MB 11.0 MB/s eta 0:00:01
|████████████████████████████▍ | 1.3 MB 11.0 MB/s eta 0:00:01
|████████████████████████████▋ | 1.3 MB 11.0 MB/s eta 0:00:01
|████████████████████████████▉ | 1.3 MB 11.0 MB/s eta 0:00:01
|█████████████████████████████ | 1.3 MB 11.0 MB/s eta 0:00:01
|█████████████████████████████▎ | 1.3 MB 11.0 MB/s eta 0:00:01
|█████████████████████████████▌ | 1.4 MB 11.0 MB/s eta 0:00:01
|█████████████████████████████▊ | 1.4 MB 11.0 MB/s eta 0:00:01
|██████████████████████████████ | 1.4 MB 11.0 MB/s eta 0:00:01
|██████████████████████████████▏ | 1.4 MB 11.0 MB/s eta 0:00:01
|██████████████████████████████▍ | 1.4 MB 11.0 MB/s eta 0:00:01
|██████████████████████████████▋ | 1.4 MB 11.0 MB/s eta 0:00:01
|██████████████████████████████▉ | 1.4 MB 11.0 MB/s eta 0:00:01
|███████████████████████████████ | 1.4 MB 11.0 MB/s eta 0:00:01
|███████████████████████████████▎| 1.4 MB 11.0 MB/s eta 0:00:01
|███████████████████████████████▌| 1.4 MB 11.0 MB/s eta 0:00:01
|███████████████████████████████▊| 1.5 MB 11.0 MB/s eta 0:00:01
|████████████████████████████████| 1.5 MB 11.0 MB/s eta 0:00:01
|████████████████████████████████| 1.5 MB 11.0 MB/s
?25hRequirement already satisfied: patsy in /usr/share/miniconda3/envs/lecture-python/lib/python3.8/site-packages (from linearmodels) (0.5.1)
Collecting property-cached>=1.6.3
Downloading property_cached-1.6.4-py2.py3-none-any.whl (7.8 kB)
Requirement already satisfied: Cython>=0.29.21 in /usr/share/miniconda3/envs/lecture-python/lib/python3.8/site-packages (from linearmodels) (0.29.21)
Requirement already satisfied: pandas>=0.24 in /usr/share/miniconda3/envs/lecture-python/lib/python3.8/site-packages (from linearmodels) (1.1.3)
Collecting mypy-extensions>=0.4
Downloading mypy_extensions-0.4.3-py2.py3-none-any.whl (4.5 kB)
Requirement already satisfied: statsmodels>=0.11 in /usr/share/miniconda3/envs/lecture-python/lib/python3.8/site-packages (from linearmodels) (0.12.0)
Collecting pyhdfe>=0.1
Downloading pyhdfe-0.1.0-py3-none-any.whl (18 kB)
Requirement already satisfied: numpy>=1.16 in /usr/share/miniconda3/envs/lecture-python/lib/python3.8/site-packages (from linearmodels) (1.19.2)
Requirement already satisfied: scipy>=1.2 in /usr/share/miniconda3/envs/lecture-python/lib/python3.8/site-packages (from linearmodels) (1.5.2)
Requirement already satisfied: six in /usr/share/miniconda3/envs/lecture-python/lib/python3.8/site-packages (from patsy->linearmodels) (1.15.0)
Requirement already satisfied: pytz>=2017.2 in /usr/share/miniconda3/envs/lecture-python/lib/python3.8/site-packages (from pandas>=0.24->linearmodels) (2020.1)
Requirement already satisfied: python-dateutil>=2.7.3 in /usr/share/miniconda3/envs/lecture-python/lib/python3.8/site-packages (from pandas>=0.24->linearmodels) (2.8.1)
Installing collected packages: property-cached, mypy-extensions, pyhdfe, linearmodels
Successfully installed linearmodels-4.22 mypy-extensions-0.4.3 property-cached-1.6.4 pyhdfe-0.1.0
57.1. Overview¶
Linear regression is a standard tool for analyzing the relationship between two or more variables.
In this lecture, we’ll use the Python package statsmodels to estimate, interpret, and visualize linear regression models.
Along the way, we’ll discuss a variety of topics, including
simple and multivariate linear regression
visualization
endogeneity and omitted variable bias
two-stage least squares
As an example, we will replicate results from Acemoglu, Johnson and Robinson’s seminal paper [AJR01].
You can download a copy here.
In the paper, the authors emphasize the importance of institutions in economic development.
The main contribution is the use of settler mortality rates as a source of exogenous variation in institutional differences.
Such variation is needed to determine whether it is institutions that give rise to greater economic growth, rather than the other way around.
Let’s start with some imports:
%matplotlib inline
import matplotlib.pyplot as plt
plt.rcParams["figure.figsize"] = (11, 5) #set default figure size
import numpy as np
import pandas as pd
import statsmodels.api as sm
from statsmodels.iolib.summary2 import summary_col
from linearmodels.iv import IV2SLS
57.2. Simple Linear Regression¶
[AJR01] wish to determine whether or not differences in institutions can help to explain observed economic outcomes.
How do we measure institutional differences and economic outcomes?
In this paper,
economic outcomes are proxied by log GDP per capita in 1995, adjusted for exchange rates.
institutional differences are proxied by an index of protection against expropriation on average over 1985-95, constructed by the Political Risk Services Group.
These variables and other data used in the paper are available for download on Daron Acemoglu’s webpage.
We will use pandas’ .read_stata() function to read in data contained in the .dta files to dataframes
df1 = pd.read_stata('https://github.com/QuantEcon/lecture-python/blob/master/source/_static/lecture_specific/ols/maketable1.dta?raw=true')
df1.head()
| shortnam | euro1900 | excolony | avexpr | logpgp95 | cons1 | cons90 | democ00a | cons00a | extmort4 | logem4 | loghjypl | baseco | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | AFG | 0.000000 | 1.0 | NaN | NaN | 1.0 | 2.0 | 1.0 | 1.0 | 93.699997 | 4.540098 | NaN | NaN |
| 1 | AGO | 8.000000 | 1.0 | 5.363636 | 7.770645 | 3.0 | 3.0 | 0.0 | 1.0 | 280.000000 | 5.634789 | -3.411248 | 1.0 |
| 2 | ARE | 0.000000 | 1.0 | 7.181818 | 9.804219 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 3 | ARG | 60.000004 | 1.0 | 6.386364 | 9.133459 | 1.0 | 6.0 | 3.0 | 3.0 | 68.900002 | 4.232656 | -0.872274 | 1.0 |
| 4 | ARM | 0.000000 | 0.0 | NaN | 7.682482 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
Let’s use a scatterplot to see whether any obvious relationship exists between GDP per capita and the protection against expropriation index
plt.style.use('seaborn')
df1.plot(x='avexpr', y='logpgp95', kind='scatter')
plt.show()
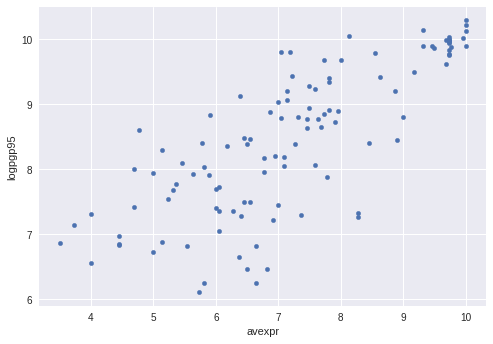
The plot shows a fairly strong positive relationship between protection against expropriation and log GDP per capita.
Specifically, if higher protection against expropriation is a measure of institutional quality, then better institutions appear to be positively correlated with better economic outcomes (higher GDP per capita).
Given the plot, choosing a linear model to describe this relationship seems like a reasonable assumption.
We can write our model as
where:
\(\beta_0\) is the intercept of the linear trend line on the y-axis
\(\beta_1\) is the slope of the linear trend line, representing the marginal effect of protection against risk on log GDP per capita
\(u_i\) is a random error term (deviations of observations from the linear trend due to factors not included in the model)
Visually, this linear model involves choosing a straight line that best fits the data, as in the following plot (Figure 2 in [AJR01])
# Dropping NA's is required to use numpy's polyfit
df1_subset = df1.dropna(subset=['logpgp95', 'avexpr'])
# Use only 'base sample' for plotting purposes
df1_subset = df1_subset[df1_subset['baseco'] == 1]
X = df1_subset['avexpr']
y = df1_subset['logpgp95']
labels = df1_subset['shortnam']
# Replace markers with country labels
fig, ax = plt.subplots()
ax.scatter(X, y, marker='')
for i, label in enumerate(labels):
ax.annotate(label, (X.iloc[i], y.iloc[i]))
# Fit a linear trend line
ax.plot(np.unique(X),
np.poly1d(np.polyfit(X, y, 1))(np.unique(X)),
color='black')
ax.set_xlim([3.3,10.5])
ax.set_ylim([4,10.5])
ax.set_xlabel('Average Expropriation Risk 1985-95')
ax.set_ylabel('Log GDP per capita, PPP, 1995')
ax.set_title('Figure 2: OLS relationship between expropriation \
risk and income')
plt.show()
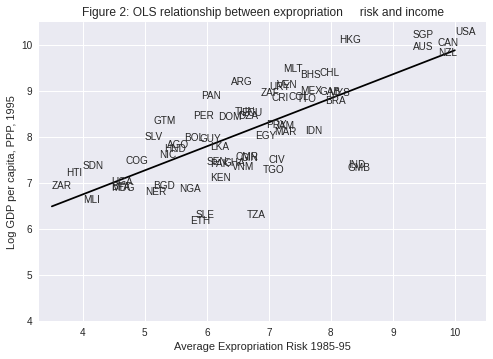
The most common technique to estimate the parameters (\(\beta\)’s) of the linear model is Ordinary Least Squares (OLS).
As the name implies, an OLS model is solved by finding the parameters that minimize the sum of squared residuals, i.e.
where \(\hat{u}_i\) is the difference between the observation and the predicted value of the dependent variable.
To estimate the constant term \(\beta_0\), we need to add a column of 1’s to our dataset (consider the equation if \(\beta_0\) was replaced with \(\beta_0 x_i\) and \(x_i = 1\))
df1['const'] = 1
Now we can construct our model in statsmodels using the OLS function.
We will use pandas dataframes with statsmodels, however standard arrays can also be used as arguments
reg1 = sm.OLS(endog=df1['logpgp95'], exog=df1[['const', 'avexpr']], \
missing='drop')
type(reg1)
statsmodels.regression.linear_model.OLS
So far we have simply constructed our model.
We need to use .fit() to obtain parameter estimates
\(\hat{\beta}_0\) and \(\hat{\beta}_1\)
results = reg1.fit()
type(results)
statsmodels.regression.linear_model.RegressionResultsWrapper
We now have the fitted regression model stored in results.
To view the OLS regression results, we can call the .summary()
method.
Note that an observation was mistakenly dropped from the results in the original paper (see the note located in maketable2.do from Acemoglu’s webpage), and thus the coefficients differ slightly.
print(results.summary())
OLS Regression Results
==============================================================================
Dep. Variable: logpgp95 R-squared: 0.611
Model: OLS Adj. R-squared: 0.608
Method: Least Squares F-statistic: 171.4
Date: Mon, 15 Mar 2021 Prob (F-statistic): 4.16e-24
Time: 23:29:02 Log-Likelihood: -119.71
No. Observations: 111 AIC: 243.4
Df Residuals: 109 BIC: 248.8
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 4.6261 0.301 15.391 0.000 4.030 5.222
avexpr 0.5319 0.041 13.093 0.000 0.451 0.612
==============================================================================
Omnibus: 9.251 Durbin-Watson: 1.689
Prob(Omnibus): 0.010 Jarque-Bera (JB): 9.170
Skew: -0.680 Prob(JB): 0.0102
Kurtosis: 3.362 Cond. No. 33.2
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
From our results, we see that
The intercept \(\hat{\beta}_0 = 4.63\).
The slope \(\hat{\beta}_1 = 0.53\).
The positive \(\hat{\beta}_1\) parameter estimate implies that. institutional quality has a positive effect on economic outcomes, as we saw in the figure.
The p-value of 0.000 for \(\hat{\beta}_1\) implies that the effect of institutions on GDP is statistically significant (using p < 0.05 as a rejection rule).
The R-squared value of 0.611 indicates that around 61% of variation in log GDP per capita is explained by protection against expropriation.
Using our parameter estimates, we can now write our estimated relationship as
This equation describes the line that best fits our data, as shown in Figure 2.
We can use this equation to predict the level of log GDP per capita for a value of the index of expropriation protection.
For example, for a country with an index value of 7.07 (the average for the dataset), we find that their predicted level of log GDP per capita in 1995 is 8.38.
mean_expr = np.mean(df1_subset['avexpr'])
mean_expr
6.515625
predicted_logpdp95 = 4.63 + 0.53 * 7.07
predicted_logpdp95
8.3771
An easier (and more accurate) way to obtain this result is to use
.predict() and set \(constant = 1\) and
\({avexpr}_i = mean\_expr\)
results.predict(exog=[1, mean_expr])
array([8.09156367])
We can obtain an array of predicted \({logpgp95}_i\) for every value
of \({avexpr}_i\) in our dataset by calling .predict() on our
results.
Plotting the predicted values against \({avexpr}_i\) shows that the predicted values lie along the linear line that we fitted above.
The observed values of \({logpgp95}_i\) are also plotted for comparison purposes
# Drop missing observations from whole sample
df1_plot = df1.dropna(subset=['logpgp95', 'avexpr'])
# Plot predicted values
fix, ax = plt.subplots()
ax.scatter(df1_plot['avexpr'], results.predict(), alpha=0.5,
label='predicted')
# Plot observed values
ax.scatter(df1_plot['avexpr'], df1_plot['logpgp95'], alpha=0.5,
label='observed')
ax.legend()
ax.set_title('OLS predicted values')
ax.set_xlabel('avexpr')
ax.set_ylabel('logpgp95')
plt.show()
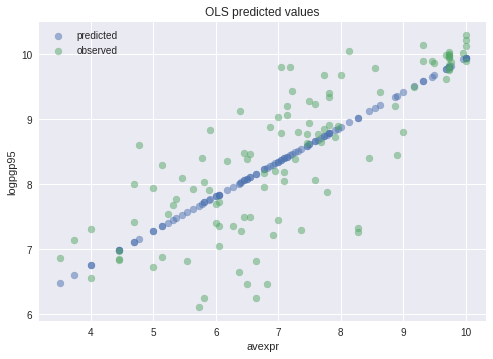
57.3. Extending the Linear Regression Model¶
So far we have only accounted for institutions affecting economic performance - almost certainly there are numerous other factors affecting GDP that are not included in our model.
Leaving out variables that affect \(logpgp95_i\) will result in omitted variable bias, yielding biased and inconsistent parameter estimates.
We can extend our bivariate regression model to a multivariate regression model by adding in other factors that may affect \(logpgp95_i\).
[AJR01] consider other factors such as:
the effect of climate on economic outcomes; latitude is used to proxy this
differences that affect both economic performance and institutions, eg. cultural, historical, etc.; controlled for with the use of continent dummies
Let’s estimate some of the extended models considered in the paper
(Table 2) using data from maketable2.dta
df2 = pd.read_stata('https://github.com/QuantEcon/lecture-python/blob/master/source/_static/lecture_specific/ols/maketable2.dta?raw=true')
# Add constant term to dataset
df2['const'] = 1
# Create lists of variables to be used in each regression
X1 = ['const', 'avexpr']
X2 = ['const', 'avexpr', 'lat_abst']
X3 = ['const', 'avexpr', 'lat_abst', 'asia', 'africa', 'other']
# Estimate an OLS regression for each set of variables
reg1 = sm.OLS(df2['logpgp95'], df2[X1], missing='drop').fit()
reg2 = sm.OLS(df2['logpgp95'], df2[X2], missing='drop').fit()
reg3 = sm.OLS(df2['logpgp95'], df2[X3], missing='drop').fit()
Now that we have fitted our model, we will use summary_col to
display the results in a single table (model numbers correspond to those
in the paper)
info_dict={'R-squared' : lambda x: f"{x.rsquared:.2f}",
'No. observations' : lambda x: f"{int(x.nobs):d}"}
results_table = summary_col(results=[reg1,reg2,reg3],
float_format='%0.2f',
stars = True,
model_names=['Model 1',
'Model 3',
'Model 4'],
info_dict=info_dict,
regressor_order=['const',
'avexpr',
'lat_abst',
'asia',
'africa'])
results_table.add_title('Table 2 - OLS Regressions')
print(results_table)
Table 2 - OLS Regressions
=========================================
Model 1 Model 3 Model 4
-----------------------------------------
const 4.63*** 4.87*** 5.85***
(0.30) (0.33) (0.34)
avexpr 0.53*** 0.46*** 0.39***
(0.04) (0.06) (0.05)
lat_abst 0.87* 0.33
(0.49) (0.45)
asia -0.15
(0.15)
africa -0.92***
(0.17)
other 0.30
(0.37)
R-squared 0.61 0.62 0.72
R-squared Adj. 0.61 0.62 0.70
R-squared 0.61 0.62 0.72
No. observations 111 111 111
=========================================
Standard errors in parentheses.
* p<.1, ** p<.05, ***p<.01
57.4. Endogeneity¶
As [AJR01] discuss, the OLS models likely suffer from endogeneity issues, resulting in biased and inconsistent model estimates.
Namely, there is likely a two-way relationship between institutions and economic outcomes:
richer countries may be able to afford or prefer better institutions
variables that affect income may also be correlated with institutional differences
the construction of the index may be biased; analysts may be biased towards seeing countries with higher income having better institutions
To deal with endogeneity, we can use two-stage least squares (2SLS) regression, which is an extension of OLS regression.
This method requires replacing the endogenous variable \({avexpr}_i\) with a variable that is:
correlated with \({avexpr}_i\)
not correlated with the error term (ie. it should not directly affect the dependent variable, otherwise it would be correlated with \(u_i\) due to omitted variable bias)
The new set of regressors is called an instrument, which aims to remove endogeneity in our proxy of institutional differences.
The main contribution of [AJR01] is the use of settler mortality rates to instrument for institutional differences.
They hypothesize that higher mortality rates of colonizers led to the establishment of institutions that were more extractive in nature (less protection against expropriation), and these institutions still persist today.
Using a scatterplot (Figure 3 in [AJR01]), we can see protection against expropriation is negatively correlated with settler mortality rates, coinciding with the authors’ hypothesis and satisfying the first condition of a valid instrument.
# Dropping NA's is required to use numpy's polyfit
df1_subset2 = df1.dropna(subset=['logem4', 'avexpr'])
X = df1_subset2['logem4']
y = df1_subset2['avexpr']
labels = df1_subset2['shortnam']
# Replace markers with country labels
fig, ax = plt.subplots()
ax.scatter(X, y, marker='')
for i, label in enumerate(labels):
ax.annotate(label, (X.iloc[i], y.iloc[i]))
# Fit a linear trend line
ax.plot(np.unique(X),
np.poly1d(np.polyfit(X, y, 1))(np.unique(X)),
color='black')
ax.set_xlim([1.8,8.4])
ax.set_ylim([3.3,10.4])
ax.set_xlabel('Log of Settler Mortality')
ax.set_ylabel('Average Expropriation Risk 1985-95')
ax.set_title('Figure 3: First-stage relationship between settler mortality \
and expropriation risk')
plt.show()
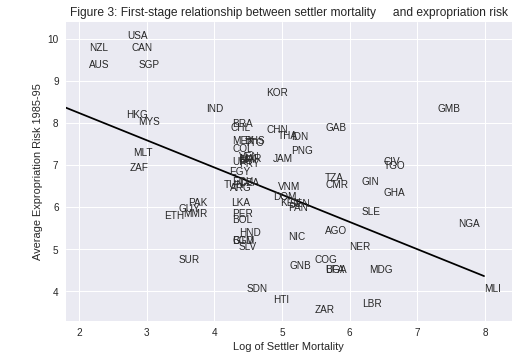
The second condition may not be satisfied if settler mortality rates in the 17th to 19th centuries have a direct effect on current GDP (in addition to their indirect effect through institutions).
For example, settler mortality rates may be related to the current disease environment in a country, which could affect current economic performance.
[AJR01] argue this is unlikely because:
The majority of settler deaths were due to malaria and yellow fever and had a limited effect on local people.
The disease burden on local people in Africa or India, for example, did not appear to be higher than average, supported by relatively high population densities in these areas before colonization.
As we appear to have a valid instrument, we can use 2SLS regression to obtain consistent and unbiased parameter estimates.
First stage
The first stage involves regressing the endogenous variable (\({avexpr}_i\)) on the instrument.
The instrument is the set of all exogenous variables in our model (and not just the variable we have replaced).
Using model 1 as an example, our instrument is simply a constant and settler mortality rates \({logem4}_i\).
Therefore, we will estimate the first-stage regression as
The data we need to estimate this equation is located in
maketable4.dta (only complete data, indicated by baseco = 1, is
used for estimation)
# Import and select the data
df4 = pd.read_stata('https://github.com/QuantEcon/lecture-python/blob/master/source/_static/lecture_specific/ols/maketable4.dta?raw=true')
df4 = df4[df4['baseco'] == 1]
# Add a constant variable
df4['const'] = 1
# Fit the first stage regression and print summary
results_fs = sm.OLS(df4['avexpr'],
df4[['const', 'logem4']],
missing='drop').fit()
print(results_fs.summary())
OLS Regression Results
==============================================================================
Dep. Variable: avexpr R-squared: 0.270
Model: OLS Adj. R-squared: 0.258
Method: Least Squares F-statistic: 22.95
Date: Mon, 15 Mar 2021 Prob (F-statistic): 1.08e-05
Time: 23:29:03 Log-Likelihood: -104.83
No. Observations: 64 AIC: 213.7
Df Residuals: 62 BIC: 218.0
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 9.3414 0.611 15.296 0.000 8.121 10.562
logem4 -0.6068 0.127 -4.790 0.000 -0.860 -0.354
==============================================================================
Omnibus: 0.035 Durbin-Watson: 2.003
Prob(Omnibus): 0.983 Jarque-Bera (JB): 0.172
Skew: 0.045 Prob(JB): 0.918
Kurtosis: 2.763 Cond. No. 19.4
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Second stage
We need to retrieve the predicted values of \({avexpr}_i\) using
.predict().
We then replace the endogenous variable \({avexpr}_i\) with the predicted values \(\widehat{avexpr}_i\) in the original linear model.
Our second stage regression is thus
df4['predicted_avexpr'] = results_fs.predict()
results_ss = sm.OLS(df4['logpgp95'],
df4[['const', 'predicted_avexpr']]).fit()
print(results_ss.summary())
OLS Regression Results
==============================================================================
Dep. Variable: logpgp95 R-squared: 0.477
Model: OLS Adj. R-squared: 0.469
Method: Least Squares F-statistic: 56.60
Date: Mon, 15 Mar 2021 Prob (F-statistic): 2.66e-10
Time: 23:29:03 Log-Likelihood: -72.268
No. Observations: 64 AIC: 148.5
Df Residuals: 62 BIC: 152.9
Df Model: 1
Covariance Type: nonrobust
====================================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------------
const 1.9097 0.823 2.320 0.024 0.264 3.555
predicted_avexpr 0.9443 0.126 7.523 0.000 0.693 1.195
==============================================================================
Omnibus: 10.547 Durbin-Watson: 2.137
Prob(Omnibus): 0.005 Jarque-Bera (JB): 11.010
Skew: -0.790 Prob(JB): 0.00407
Kurtosis: 4.277 Cond. No. 58.1
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
The second-stage regression results give us an unbiased and consistent estimate of the effect of institutions on economic outcomes.
The result suggests a stronger positive relationship than what the OLS results indicated.
Note that while our parameter estimates are correct, our standard errors are not and for this reason, computing 2SLS ‘manually’ (in stages with OLS) is not recommended.
We can correctly estimate a 2SLS regression in one step using the
linearmodels package, an extension of statsmodels
Note that when using IV2SLS, the exogenous and instrument variables
are split up in the function arguments (whereas before the instrument
included exogenous variables)
iv = IV2SLS(dependent=df4['logpgp95'],
exog=df4['const'],
endog=df4['avexpr'],
instruments=df4['logem4']).fit(cov_type='unadjusted')
print(iv.summary)
IV-2SLS Estimation Summary
==============================================================================
Dep. Variable: logpgp95 R-squared: 0.1870
Estimator: IV-2SLS Adj. R-squared: 0.1739
No. Observations: 64 F-statistic: 37.568
Date: Mon, Mar 15 2021 P-value (F-stat) 0.0000
Time: 23:29:04 Distribution: chi2(1)
Cov. Estimator: unadjusted
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
const 1.9097 1.0106 1.8897 0.0588 -0.0710 3.8903
avexpr 0.9443 0.1541 6.1293 0.0000 0.6423 1.2462
==============================================================================
Endogenous: avexpr
Instruments: logem4
Unadjusted Covariance (Homoskedastic)
Debiased: False
Given that we now have consistent and unbiased estimates, we can infer from the model we have estimated that institutional differences (stemming from institutions set up during colonization) can help to explain differences in income levels across countries today.
[AJR01] use a marginal effect of 0.94 to calculate that the difference in the index between Chile and Nigeria (ie. institutional quality) implies up to a 7-fold difference in income, emphasizing the significance of institutions in economic development.
57.5. Summary¶
We have demonstrated basic OLS and 2SLS regression in statsmodels and linearmodels.
If you are familiar with R, you may want to use the formula interface to statsmodels, or consider using r2py to call R from within Python.
57.6. Exercises¶
57.6.1. Exercise 1¶
In the lecture, we think the original model suffers from endogeneity bias due to the likely effect income has on institutional development.
Although endogeneity is often best identified by thinking about the data and model, we can formally test for endogeneity using the Hausman test.
We want to test for correlation between the endogenous variable, \(avexpr_i\), and the errors, \(u_i\)
This test is running in two stages.
First, we regress \(avexpr_i\) on the instrument, \(logem4_i\)
Second, we retrieve the residuals \(\hat{\upsilon}_i\) and include them in the original equation
If \(\alpha\) is statistically significant (with a p-value < 0.05), then we reject the null hypothesis and conclude that \(avexpr_i\) is endogenous.
Using the above information, estimate a Hausman test and interpret your results.
57.6.2. Exercise 2¶
The OLS parameter \(\beta\) can also be estimated using matrix
algebra and numpy (you may need to review the
numpy lecture to
complete this exercise).
The linear equation we want to estimate is (written in matrix form)
To solve for the unknown parameter \(\beta\), we want to minimize the sum of squared residuals
Rearranging the first equation and substituting into the second equation, we can write
Solving this optimization problem gives the solution for the \(\hat{\beta}\) coefficients
Using the above information, compute \(\hat{\beta}\) from model 1
using numpy - your results should be the same as those in the
statsmodels output from earlier in the lecture.
57.7. Solutions¶
57.7.1. Exercise 1¶
# Load in data
df4 = pd.read_stata('https://github.com/QuantEcon/lecture-python/blob/master/source/_static/lecture_specific/ols/maketable4.dta?raw=true')
# Add a constant term
df4['const'] = 1
# Estimate the first stage regression
reg1 = sm.OLS(endog=df4['avexpr'],
exog=df4[['const', 'logem4']],
missing='drop').fit()
# Retrieve the residuals
df4['resid'] = reg1.resid
# Estimate the second stage residuals
reg2 = sm.OLS(endog=df4['logpgp95'],
exog=df4[['const', 'avexpr', 'resid']],
missing='drop').fit()
print(reg2.summary())
OLS Regression Results
==============================================================================
Dep. Variable: logpgp95 R-squared: 0.689
Model: OLS Adj. R-squared: 0.679
Method: Least Squares F-statistic: 74.05
Date: Mon, 15 Mar 2021 Prob (F-statistic): 1.07e-17
Time: 23:29:04 Log-Likelihood: -62.031
No. Observations: 70 AIC: 130.1
Df Residuals: 67 BIC: 136.8
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 2.4782 0.547 4.530 0.000 1.386 3.570
avexpr 0.8564 0.082 10.406 0.000 0.692 1.021
resid -0.4951 0.099 -5.017 0.000 -0.692 -0.298
==============================================================================
Omnibus: 17.597 Durbin-Watson: 2.086
Prob(Omnibus): 0.000 Jarque-Bera (JB): 23.194
Skew: -1.054 Prob(JB): 9.19e-06
Kurtosis: 4.873 Cond. No. 53.8
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
The output shows that the coefficient on the residuals is statistically significant, indicating \(avexpr_i\) is endogenous.
57.7.2. Exercise 2¶
# Load in data
df1 = pd.read_stata('https://github.com/QuantEcon/lecture-python/blob/master/source/_static/lecture_specific/ols/maketable1.dta?raw=true')
df1 = df1.dropna(subset=['logpgp95', 'avexpr'])
# Add a constant term
df1['const'] = 1
# Define the X and y variables
y = np.asarray(df1['logpgp95'])
X = np.asarray(df1[['const', 'avexpr']])
# Compute β_hat
β_hat = np.linalg.solve(X.T @ X, X.T @ y)
# Print out the results from the 2 x 1 vector β_hat
print(f'β_0 = {β_hat[0]:.2}')
print(f'β_1 = {β_hat[1]:.2}')
β_0 = 4.6
β_1 = 0.53
It is also possible to use np.linalg.inv(X.T @ X) @ X.T @ y to solve
for \(\beta\), however .solve() is preferred as it involves fewer
computations.
